队列&栈

发表于 | Edited on

介绍

  1. 了解FIFO和LIFO处理顺序的原理
  2. 实现这两个数据结构
  3. 熟悉内置的队列和栈结构
  4. 解决基本的队列相关问题，尤其是BFS
  5. 解决基本的栈相关问题
  6. 理解当你使用 DFS 和其他递归算法来解决问题时，系统栈是如何帮助你的。

队列：先入先出的数据结构

  1. 理解FIFO和队列的定义；
  2. 能够自己实现队列；
  3. 熟悉内置队列结构；
  4. 使用队列来解决简单的问题；

队列

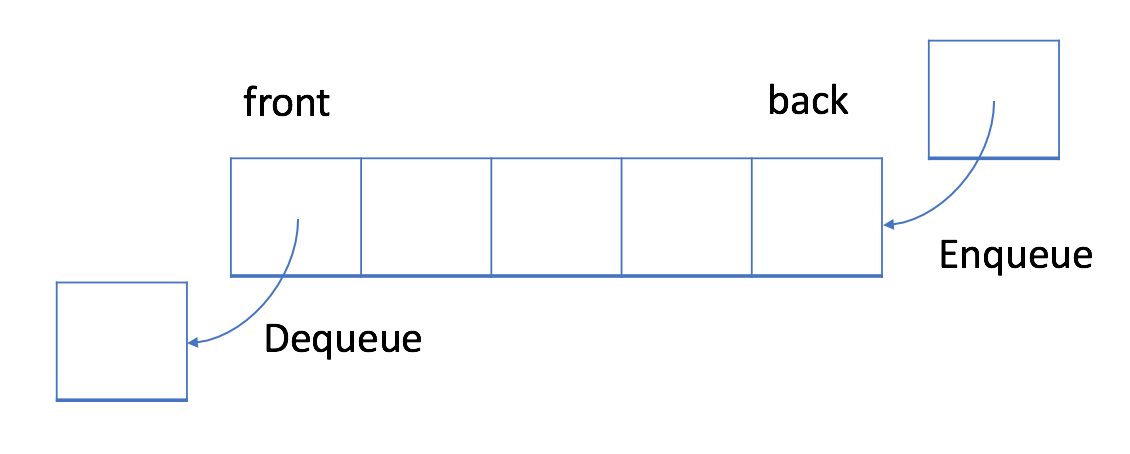
在FIFO数据结构中，将首先处理添加到队列中的第一个元素。 插入（insert）操作也称为入队（enqueue），新元素始终被添加在队列的末尾。删除（delete）操作也被称为出队（dequeue）。你只能移除第一个元素。

队列-实现

为了实现队列，我们可以使用动态数组和指向队列头部的索引。

如上所述，队列应支持两种操作：入队和出队。入队会向队列追加一个新元素，而出队会删除第一个元素。 所以我们需要一个索引来指出起点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class MYQueue {
    private List<Integer> data;
    private int p_start;
    public MyQueue() {
        data = new ArrayList<Integer>();
        p_start = 0;
    }

    public boolean enQueue(int x) {
        data.add(x);
        return true;
    }

    public boolean deQueue() {
        if (isEmpty() == true) {
            return false;
        }
        p_start++;
        return true;
    }

    public int Front() {
        return data.get(p_start);
    }

    public boolean isEmpty() {
        return p_start >= data.size();
    }
}

循环队列

此前，简单但是低效的队列实现。
更有效的方法是使用循环队列。使用固定大小的数组和两个指针来指示起始位置和结束位置。目的是重用之前被浪费的存储。

循环队列的实现：

  1. 初始化queue，设置queue的maxSize，head和tail节点
  2. 入队enqueue：检查元素个数是否是maxSize-1；
    • Yes，返回Queue满了
    • No，在tail的位置上增加新元素，并增加tail节点
  3. 出队dequeu：检查队列中个数是否为0
    • Yes，返回Queue是空
    • No，减少head节点
  4. 找size：
    • tail >= head， size = (tail - head) + 1
    • head > tail, size = maxSize - (head - tail) + 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
class MyCircularQueue {
    int data[];
    int p_start;
    int p_end;

    /** Initialize your data structure here. Set the size of the queue to be k. */
    public MyCircularQueue(int k) {
        data = new int[k];
        p_start = -1;
        p_end = -1;
    }

    /** Insert an element into the circular queue. Return true if the operation is successful. */
    public boolean enQueue(int value) {
        if (isFull()) {
            return false;
        } else {
            if (p_start == -1) {
                p_start = 0;
            }
            p_end = (p_end + 1) % (data.length);
            data[p_end] = value;
            return true;
        }
    }

    /** Delete an element from the circular queue. Return true if the operation is successful. */
    public boolean deQueue() {
        int y;
        if (isEmpty()) {
            return false;
        } else {
            y = data[p_start];
            if (p_start == p_end) {
                p_start = -1;
                p_end = -1;
            } else {
                p_start = (p_start + 1) % data.length;
            }
            return true;
        }
    }

    /** Get the front item from the queue. */
    public int Front() {
        if (isEmpty()) {
            return -1;
        }
        return data[p_start];
    }

    /** Get the last item from the queue. */
    public int Rear() {
        if (isEmpty()) {
            return -1;
        }
        return data[p_end];
    }

    /** Checks whether the circular queue is empty or not. */
    public boolean isEmpty() {
        if (p_start == -1) {
            return true;
        }
        return false;
    }

    /** Checks whether the circular queue is full or not. */
    public boolean isFull() {
        if(p_start  == 0 && p_end == data.length - 1) {
            return true;
        }
        if (p_start == p_end + 1) {
            return true;
        }
        return false;
    }
}

/**
 * Your MyCircularQueue object will be instantiated and called as such:
 * MyCircularQueue obj = new MyCircularQueue(k);
 * boolean param_1 = obj.enQueue(value);
 * boolean param_2 = obj.deQueue();
 * int param_3 = obj.Front();
 * int param_4 = obj.Rear();
 * boolean param_5 = obj.isEmpty();
 * boolean param_6 = obj.isFull();
 */

队列和BFS（breadth-first-search）

广度优先搜索（BFS）是一个常见应用是找出从根结点到目标结点的最短路径。

  1. 结点的处理顺序
    第一轮中，处理根结点；第二轮中，处理根结点旁边的结点；在第三轮中，处理距根结点两步的结点；等等
    与树的层序遍历类似，越是接近根结点的结点将越早地遍历。
    如果在第k轮中将结点X添加到队列中，则根节点与X之间的最短路径的长度恰好是k。也就是说，第一次找到目标结点时，你已经处于最短路径中。
  2. 队列的入队和出队顺序是什么？
    首先将根节点排入队列。在每一轮中，逐个处理已经在队列中的结点，并将所有邻居添加到队列中。新添加的结点不会立即遍历，而是在下一轮中处理。
    结点的处理顺序与它们添加到队列的顺序是完全相同的顺序，即先进先出

广度优先搜索-模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * 返回根结点到目标结点的最短路径
 */
int BFS(Node root, Node target) {
    Queue<Node> queue; //保存所有待处理的所有结点
    int step = 0; //从根结点到当前结点的步数
    //初始化
    add root to queue;
    while (queue is not empty) {
        step = step + 1;
        //遍历在队列总的结点
        int size = queue.size();
        for (int i = 0; i < size; ++i) {
            Node cur = this first node in queue;
            return step if cur is target;
            for (Node next : the neighbors of cur) {
                add next to queue;
            }
            remove the first node from queue;
        }
    }
    return -1;

}
  1. 每一轮中，队列中的节点是等待处理的结点。
  2. 在每个更外一层的while循环之后，我们距离根结点更远一步。遍历step指示从根结点到正在访问的当前结点的距离。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int BFS(Node root, Node target) {
    Queue<Node> queue;
    Set<Node> used; //保存所有已经使用过的结点
    int step = 0;
    //初始化
    add root to queue;
    add root to used;
    //BFS
    while (queue is not empty) {
        step = step + 1;
        int size = queue.size();
        for (int i = 0； i < size; ++i) {
            Node cur = this first node in queue;
            return step if cur is target;
            for (Node next : this neighbors of cur) {
                if (next is not in used) {
                    add next to queue;
                    add next to used;
                }
            }
            remove the first node from queue;
        }
    }
    return -1;

}

200.岛屿的个数

算法：广度优先搜索

线性扫描整个二维网络，如果一个结点包含1，则以其为根节点启动广度优先搜索。将其放入队列中，（上下左右都得设置入队）并将值设为0以标记访问过该结点。迭代地搜索队列中每个结点，直到队列为空。

752.打开转盘锁

完全平方数

对问题建模：将整个问题变成一个图论问题。

从n到0，每个数字代表一个节点；
如果两个数x到y相差一个完全平方数，则连接一条边；
就得到了一个无权图；

原来的问题就转化为，在这个无权图中找出从n到0的最短路径，所以需要BFS来完成

栈

后入先出的数据结构

栈

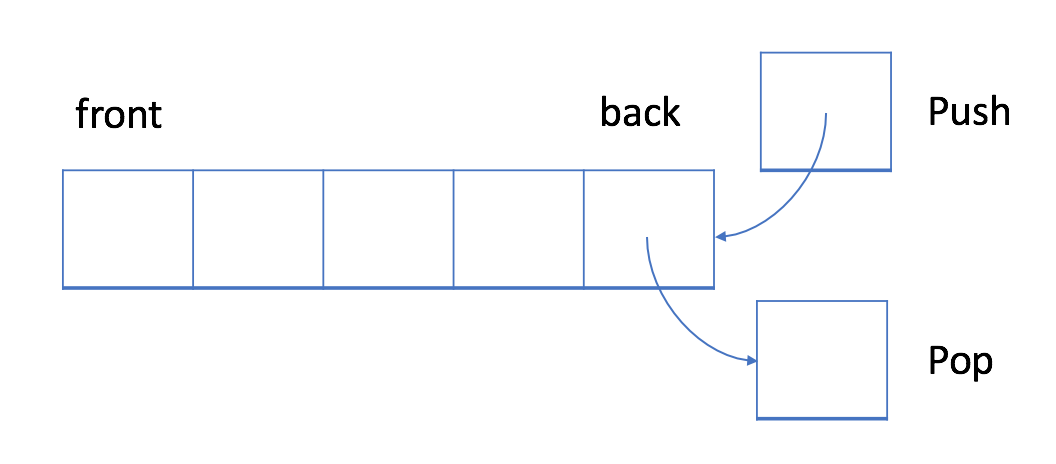
在LIFO数据结构中，将首先处理添加到队列中的最新元素。

与队列不同，栈是一个LIFO数据结构。通常，插入操作在栈中被称作入栈push。与队列类似，总是在堆栈的末尾添加一个新元素。但是，删除操作，退栈pop，将始终删除队列中相对于它的最后一个元素。

实现-栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class MyStack {
    private List<Integer> data;
    public MyStack() {
        data = new ArrayList<>();
    }

    public void push(int x) {
        data.add(x);
    }

    public boolean isEmpty() {
        return data.isEmpty();
    }

    public int top() {
        return data.get(data.size() - 1);
    }

    public boolean pop() {
        is(isEmpty()) {
            return false;
        }
        data.remove(data.size() - 1);
        return true;
    }
}

最小栈

两个栈，一个数据栈，一个辅助栈

有效的括号

在表示问题的递归结构时，栈数据结构可以派上用场。我们无法真正地从内到外处理这个问题，因为我们对整体结构一无所知。但是，栈可以帮助我们递归地处理这种情况，即从外部到内部。

  1. 初始化栈
  2. 一次处理表达式的每个括号
  3. 如果遇到开括号，我们只需将其推到栈即可。这意味着我们将稍后处理它。
  4. 如果遇到一个闭括号，那么我们检查栈顶元素。如果栈顶元素是一个相同类型的左括号，那么我们将它从栈中弹出并继续处理。否则，这意味着表达式无效。
  5. 如果到最后我们剩下的栈中仍然有元素，那么这意味着表达式无效。

每日温度

逆序遍历，为什么要使用逆序遍历。因为正常遍历思路，遍历到当前天，你无法知道后面几天的温度情况。
逆序遍历，后面几天的温度情况已经知晓，很容易得到经过几天后的温度比今天温度高。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int[] dailyTemperatures(int[] T) {
        int[] res = new int[T.length];
        // 单调栈 里面的数 非递增排序 
        Stack<Integer> stack = new Stack();
        // 从后往前遍历
        for(int i = T.length-1; i >= 0; i--){
            // 当前元素比栈顶元素大 出栈 重新调整栈直至满足要求
            while(!stack.isEmpty() && T[i] >= T[stack.peek()]){
                stack.pop();
            }
            // 栈为空 即后面没有比当前天温度高的
            // 不为空 栈顶元素对应的下标减去当前下标即为经过几天后温度比当前天温度高
            res[i] = stack.isEmpty()? 0 :stack.peek()-i;
            // 当前元素进栈
            stack.push(i);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
        T = [73,74,75,71,69,72,76,73]

第一次遍历: i = 7, T[i] = 73, stack = []
        最后一天，后面没有比今天温度高的 res[7] = 0 ,stack = [7]

第二次遍历: i = 6, T[i] = 76, stack = [7]
        栈顶对应的温度T[7]=73,76>73,出栈,此时栈为空,加入6,res[6] = 0, stack = [6]

第三次遍历: i = 5, T[i] = 72, stack = [6]
        栈顶对应的温度T[6]=76,满足要求,计算结果后入栈。res[5] = 6-5, stack = [6,5]

第四次遍历: i = 4, T[i] = 69, stack = [6,5]
        栈顶对应的温度T[5]=72,满足要求,计算结果后入栈。res[4] = 5-4, stack = [6,5,4]

第五次遍历: i = 3, T[i] = 71, stack = [6,5,4]
        栈顶对应的温度T[4]=69,71>69,出栈。stack = [6,5]
        栈顶对应的温度T[5]=72,满足要求,计算结果后入栈。res[3] = 5-3, stack = [6,5,3]

第六次遍历: i = 2, T[i] = 75, stack = [6,5,3]
        栈顶对应的温度T[3]=71,75>71,出栈。stack = [6,5]
        栈顶对应的温度T[5]=72,75>72,出栈。stack = [6]
        栈顶对应的温度T[6]=76,满足要求,计算结果后入栈。res[2] = 6-2, stack = [6,2]

第七次遍历: i = 1, T[i] = 74, stack = [6,2]
        栈顶对应的温度T[2]=75,满足要求,计算结果后入栈。res[1] = 2-1, stack = [6,2,1]

第八次遍历: i = 0, T[i] = 73, stack = [6,2,1]
        栈顶对应的温度T[1]=74,满足要求,计算结果后入栈。res[0] = 1-0, stack = [6,2,1,0]

遍历结束: res = [1,1,4,2,1,1,0,0]
0%